HW 02 --- Lecture 11 Q&A

HW 02

1

Q2这题，一开始自己做的时候没有做出来，尝试了很多次都没能成功，

于是就去看了提示视频，然后助教老师说道，可以写一个 helper 函数来追踪需要的信息

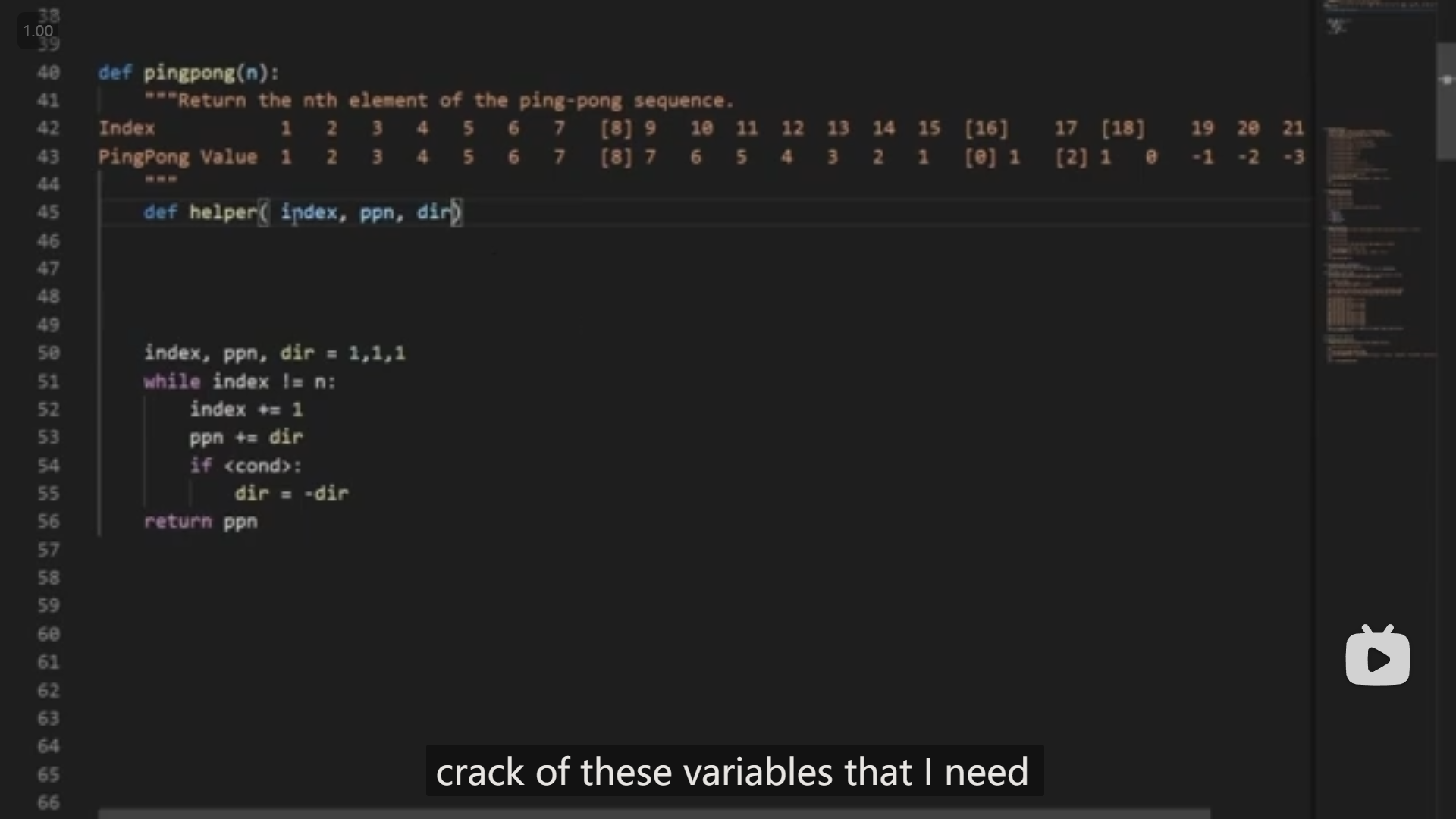
于是看到这里我大概就有思路了，最后就完成了

代码

def pingpong(n):
    "*** YOUR CODE HERE ***"
    def helper(index, pingpong_num, direction):
        if index == n:
            return pingpong_num + direction
        else:
            return helper(index + 1, pingpong_num + direction, direction * (-1 if index % 8 == 0 or num_eights(index) else 1))
    return helper(1, 0, 1)

2

Q4这题，感觉和第9节Tree Recursion课上最后展示的例子很像，

但是一开始也是没做出这题，之后发现需要写一个 helper 函数来辅助记录信息，最后仿照上图例子的大致结构就写出来了

代码

def count_coins(total):
    "*** YOUR CODE HERE ***"
    def helper(index, largest_coin):
        if index == total:
            return 1
        elif index > total:
            return 0
        elif largest_coin == None:
            return 0
        else:
            return helper(index + largest_coin, largest_coin) + helper(index, next_largest_coin(largest_coin))
    return helper(0, 1)

3

Q5这题没有想出来，最后是在网上找到了差不多的( lambda 函数递归的)代码，

def make_anonymous_factorial():
    return (lambda f: lambda n: f(f, n))(lambda f, i: 1 if i == 0 else i * f(f, i - 1))

后来再回来看这个代码，大概能理解为什么要这么做了，由于递归需要调用自己，所以在 lambda 函数中只能借助外部，通过参数把自己传进来(通过参数来传递信息比较常见)，所以核心部分就写成了

(lambda f, i: 1 if i == 0 else i * f(f, i - 1))

剩下的部分就是去开始递归的过程。

---

在第12节的Q&A中也有人问到了这一题，John也进行了解答

Lecture 10 Containers

1

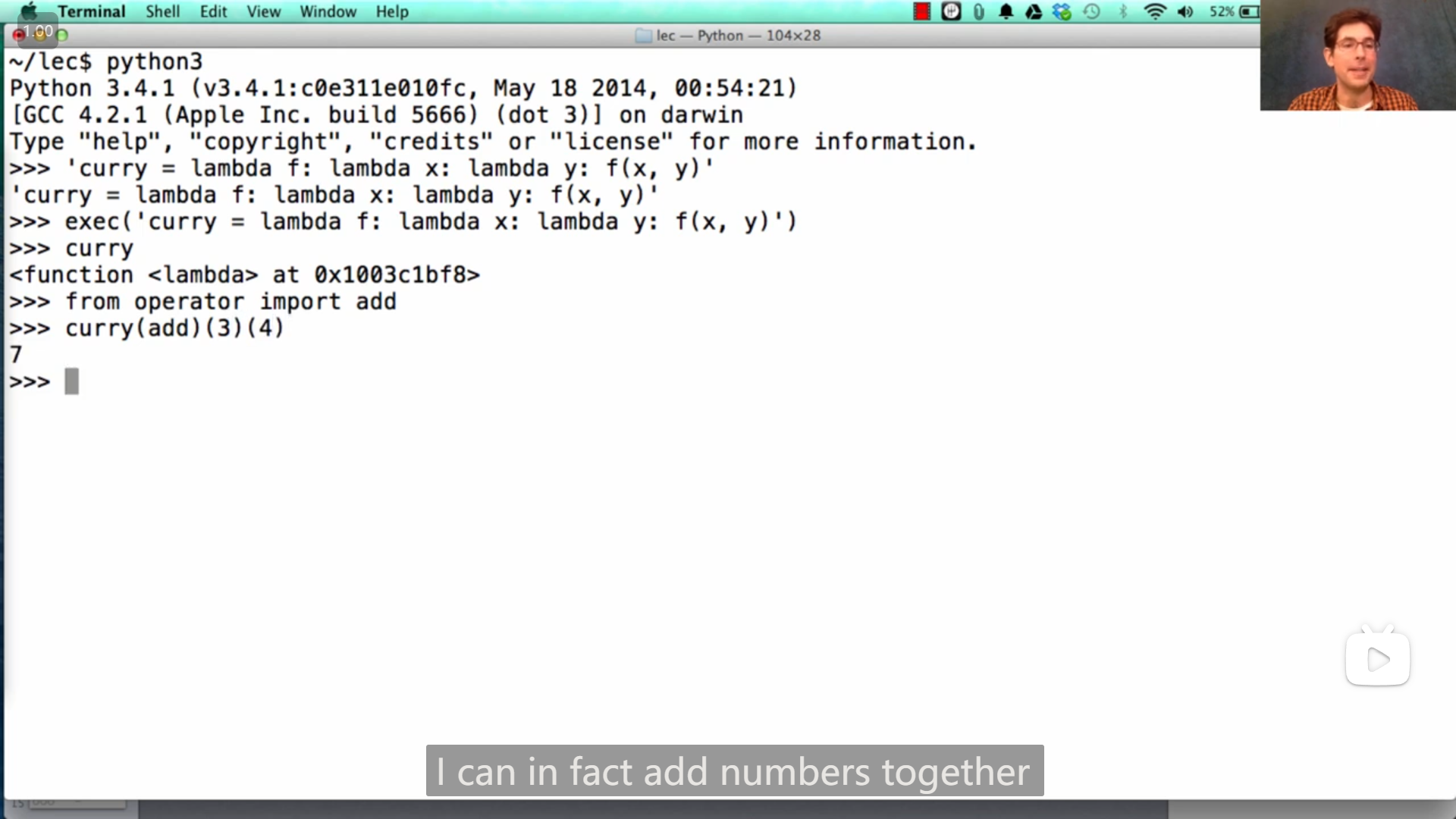
exec() 函数可以执行字符串中的语句，如

exec("curry = lambda f: lambda x: lambda y: f(x, y)")

可以让 curry 变量指向一个匿名函数

2

例

for _ in range(3):
    ...

可以用 _ 变量表示 for 循环中执行的语句与迭代的变量无关

3

string字符串的元素也是字符串，list的元素就是元素，即有

>>> str = "hello"
>>> str[3][0][0]
'l'

4

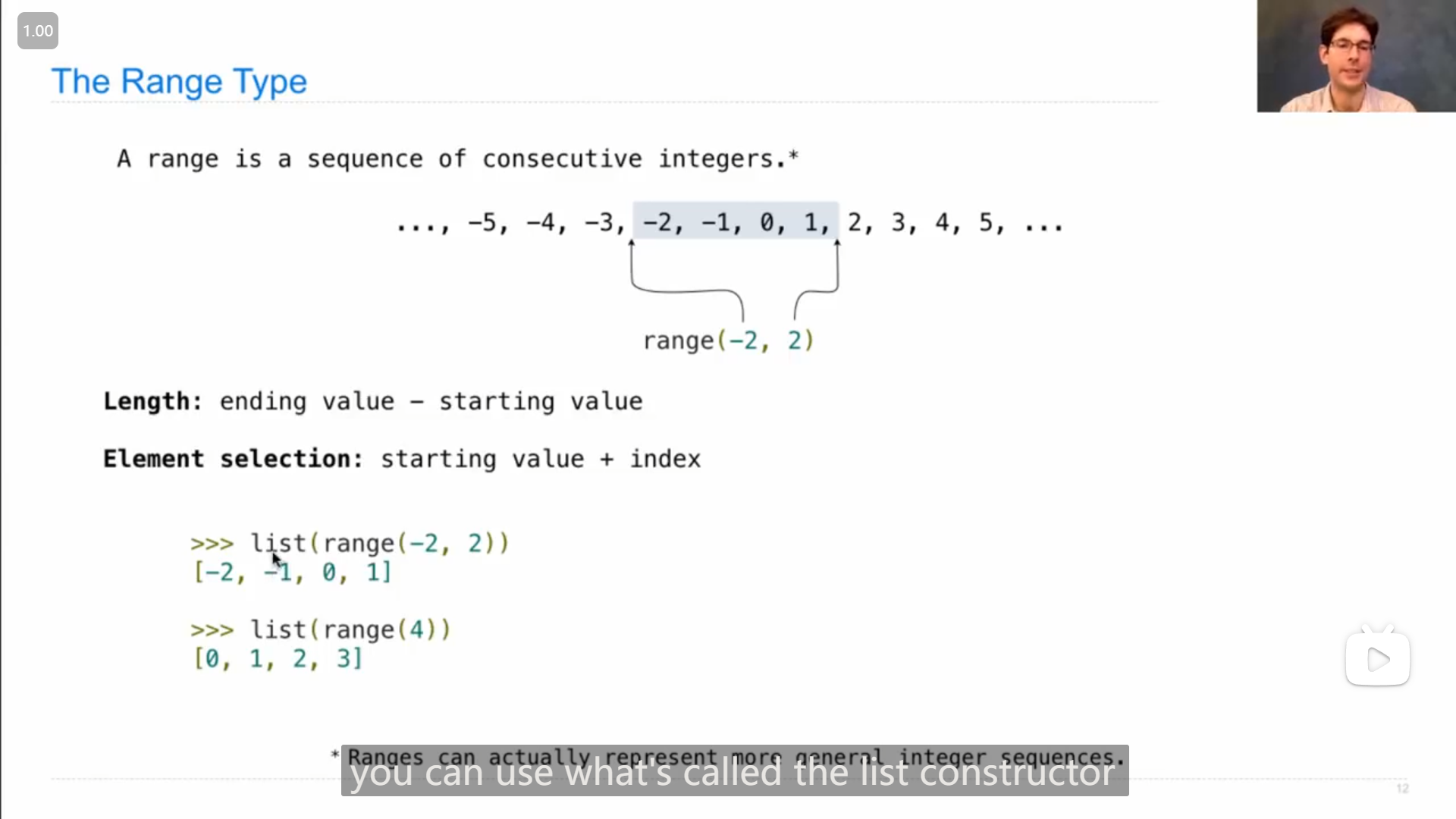
记忆技巧 “下标” 对应元素之前，

对有序结构切片也适用，其中的负数也适用，如

>>> l = list(range(5))
>>> l
[0, 1, 2, 3, 4]
>>> l[1:-1]
[1, 2, 3]

5

列表推导式(list comprehension)可以用 if ：

>>> l2 = [x for x in [0, 1, 2, 5, 6] if x % 3 == 0]
>>> l2
[0, 6]

6

如果列表有子列表，且元素个数都固定，那么 for 可以直接获取子列表的元素/unpack子列表，如子列表都含两个元素：

Lecture 10 Q&A

1

递增的递归写阶乘：

def fact(n):
    return fact_helper(n, 1, 1)

def fact_helper(n, k, result):
    """Computes k * (k + 1) * (k + 2) * ... * n
    by accumulating the result
    """
    if n == k:
        return k * result
    else:
        return fact_helper(n, k + 1, k * result)

or

def fact(n, k=1, result=1):
    """Computes k * (k + 1) * (k + 2) * ... * n
    by accumulating the result
    """
    if n == k:
        return k * result
    else:
        return fact(n, k + 1, k * result)

这种(递增的递归)更像循环语句

(也可以将helper写入函数内部)

def fact(n):
    def helper(k, result):
        if k == n:
            return k * result
        else:
            return helper(k + 1, k * result)
    return helper(1, 1)

or

def fact(n):
    def helper(k):
        if k == n:
            return k
        else:
            return k * helper(k + 1)
    return helper(1)

Lab 04

lab04中的Q4-Q6 在掌握了 假想函数能返回所需要返回的东西(即假想返回的东西是已知的) 的诀窍(在lecture12中)之后，做的很顺畅。

1. 先假想函数能返回所需的东西/值
2. 再想如何把情况分解成另一个或几个差不多(形式一样)但简单了一点的情况(有点类似于动态规划的找递推式)，如Q4中一般情况可以分成两个行/列减一的情况(即向上或向右走一步)
3. 再想 “基本情况” (最简单/特殊的情况(作为递归的终止情况))
4. 最后调整一般情况的返回的值

代码

Q4

def paths(m, n):
    """Return the number of paths from one corner of an
    M by N grid to the opposite corner.

    >>> paths(2, 2)
    2
    >>> paths(5, 7)
    210
    >>> paths(117, 1)
    1
    >>> paths(1, 157)
    1
    """
    "*** YOUR CODE HERE ***"
    if m == 1 or n == 1:
        return 1
    else:
        return paths(m - 1, n) + paths(m, n - 1)

Q5

def max_subseq(n, t):
    """
    Return the maximum subsequence of length at most t that can be found in the given number n.
    For example, for n = 20125 and t = 3, we have that the subsequences are
        2
        0
        1
        2
        5
        20
        21
        22
        25
        01
        02
        05
        12
        15
        25
        201
        202
        205
        212
        215
        225
        012
        015
        025
        125
    and of these, the maxumum number is 225, so our answer is 225.

    >>> max_subseq(20125, 3)
    225
    >>> max_subseq(20125, 5)
    20125
    >>> max_subseq(20125, 6) # note that 20125 == 020125
    20125
    >>> max_subseq(12345, 3)
    345
    >>> max_subseq(12345, 0) # 0 is of length 0
    0
    >>> max_subseq(12345, 1)
    5
    """
    "*** YOUR CODE HERE ***"
    if t == 0:
        return 0
    elif n < 10:
        return n
    else:
        return max(max_subseq(n // 10, t - 1) * 10 + n % 10, max_subseq(n // 10, t))

Q6

def add_chars(w1, w2):
    """
    Return a string containing the characters you need to add to w1 to get w2.

    You may assume that w1 is a subsequence of w2.

    >>> add_chars("owl", "howl")
    'h'
    >>> add_chars("want", "wanton")
    'on'
    >>> add_chars("rat", "radiate")
    'diae'
    >>> add_chars("a", "prepare")
    'prepre'
    >>> add_chars("resin", "recursion")
    'curo'
    >>> add_chars("fin", "effusion")
    'efuso'
    >>> add_chars("coy", "cacophony")
    'acphon'
    >>> from construct_check import check
    >>> # ban iteration and sets
    >>> check(LAB_SOURCE_FILE, 'add_chars',
    ...       ['For', 'While', 'Set', 'SetComp']) # Must use recursion
    True
    """
    "*** YOUR CODE HERE ***"
    if not w1:
        return w2
    elif w1[0] == w2[0]:
        return add_chars(w1[1:], w2[1:])
    else:
        return w2[0] + add_chars(w1, w2[1:])

Lecture 11 Data Abstraction

1

"Unpacking" a list

2

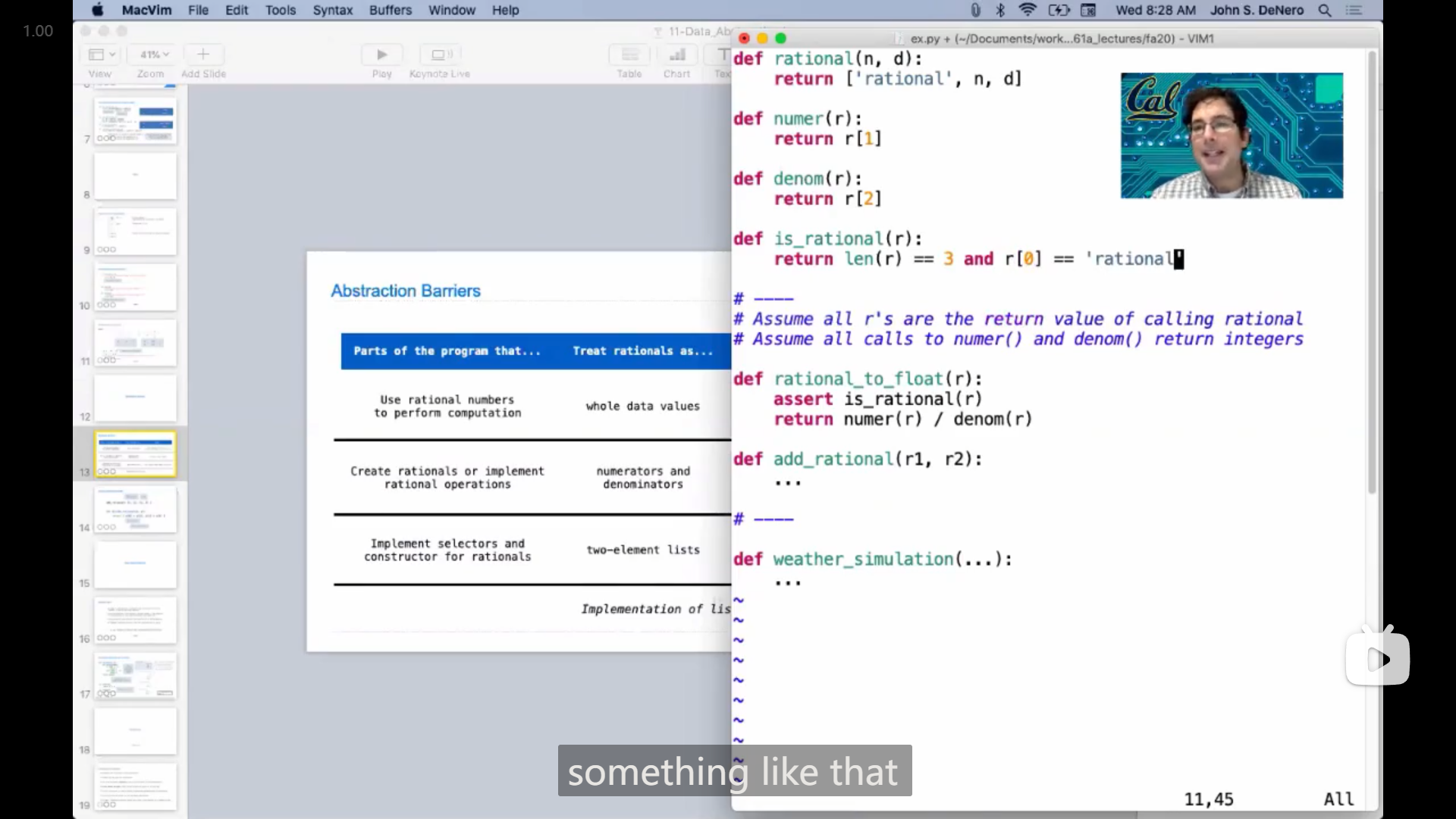
抽象思想

... you should know that when you're writing one part of a large program, that it should use the level abstraction appropriate to what you're trying to do,

and the higher you stay up, without crossing of these boundaries, the easier it will be to change your program

要 向下解构，和 向上抽象

3

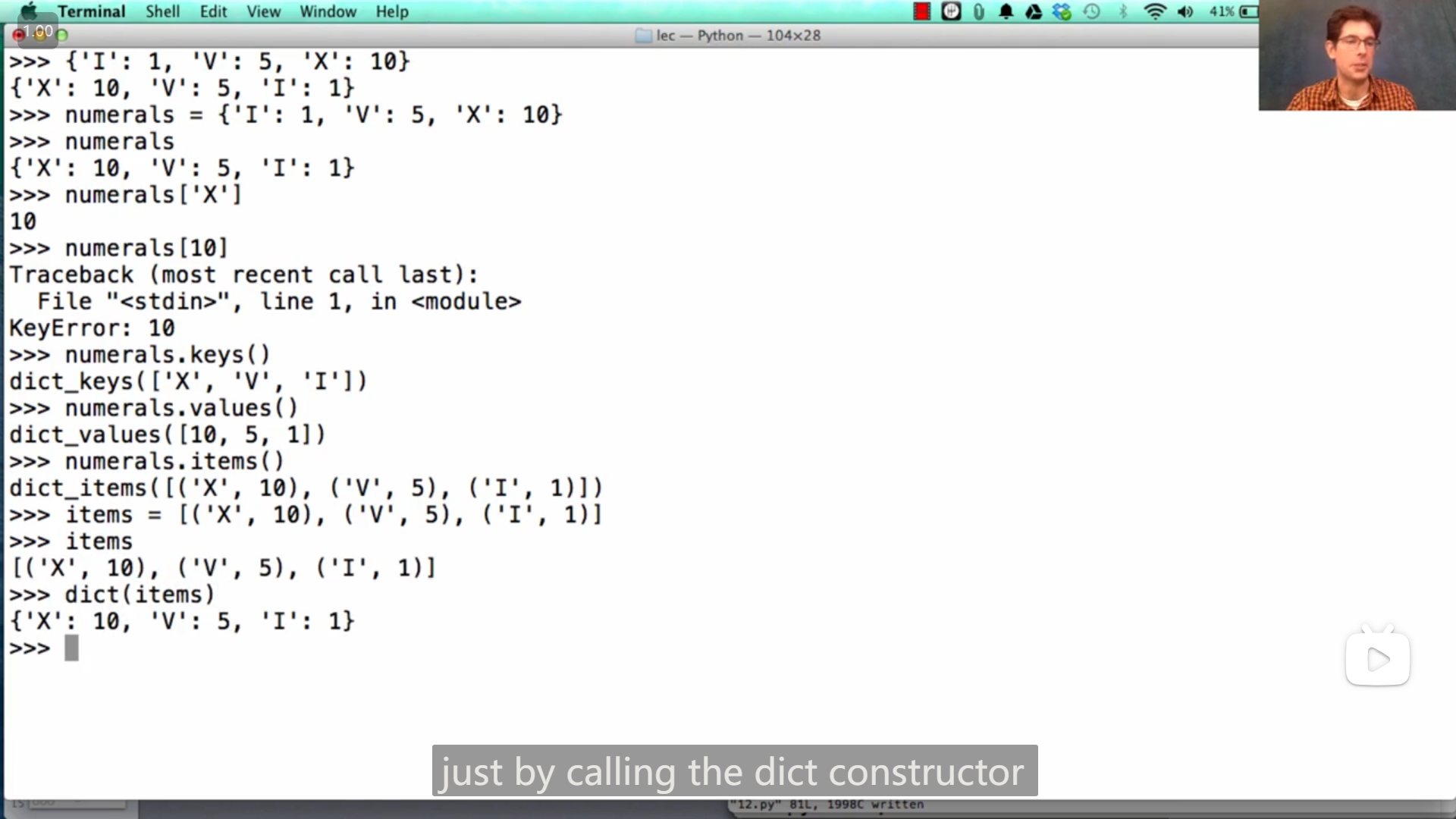
字典可以通过特定的列表构造( 二元元组 组成的列表)

4

字典也有推导式

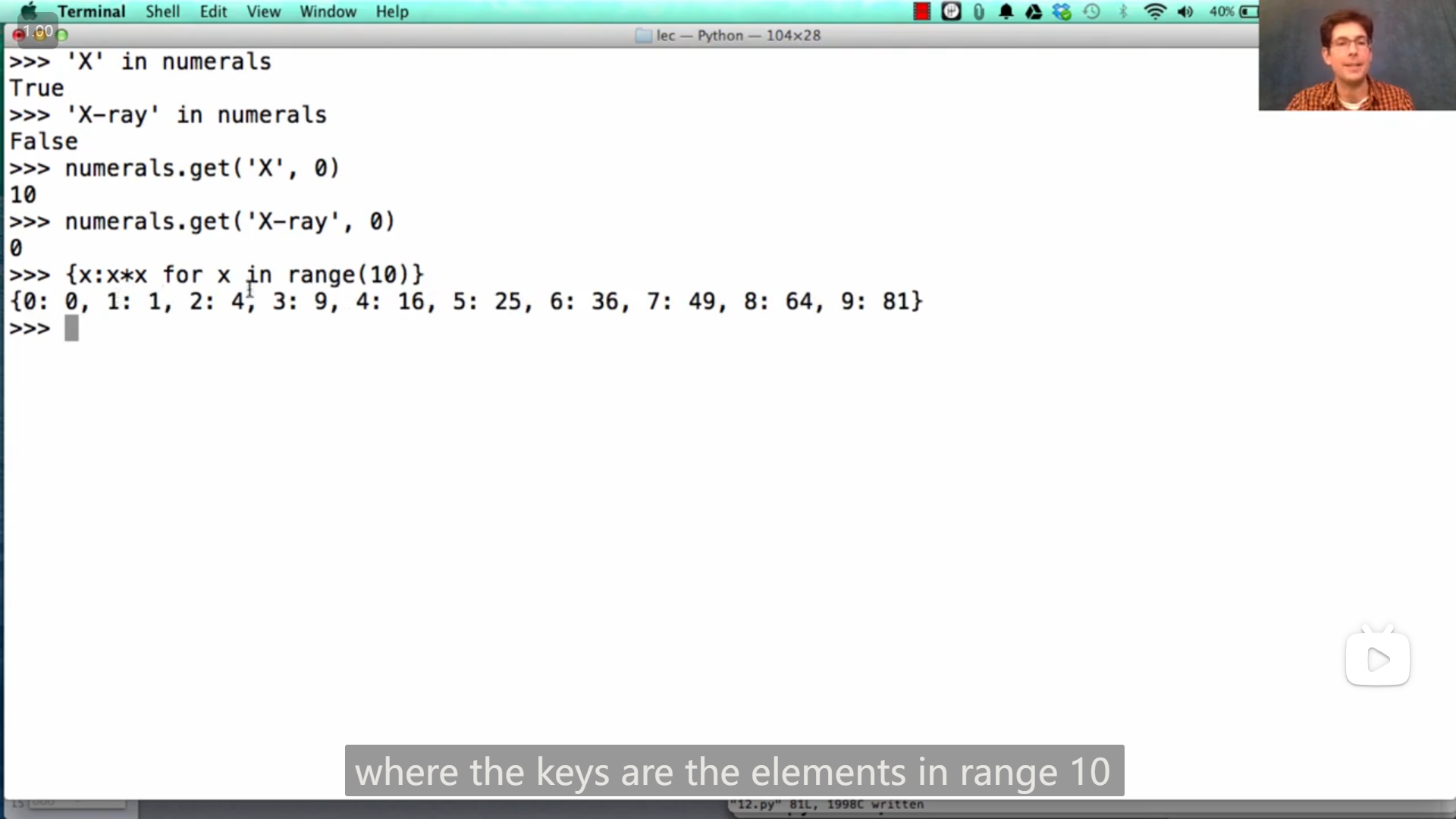
Lecture 11 Q&A

1

抽象可以使得修改某一层(layer)代码时带来的冲击/影响被隔离(isolate the impact)，有时可以使得修改所产生的影响只在这一层上。

冲击被隔离的例子：python dictionary的底层代码经常改变，但并不影响python中的使用

2

添加判断功能可以这样设计